Как машинное обучение помогает роботам обходить препятствия

Проблема поиска пути (траектории) естественным образом возникает в самых различных приложениях, таких как робототехника, видеоигры и многие другие. В наиболее распространенной постановке нас интересует кратчайший путь, огибающий препятствия. В ИИ эта проблема часто сводится к поиску пути на графе, представляющем рабочее пространство агента. Для этого подхода рабочее пространство сначала отображается в сетчатый граф, то есть некоторую регулярную структуру, состоящую из узлов и ребер. Чаще всего для этого используют 8-связный граф, который представляет собой квадратную решетку. Затем вызывается какой либо поисковый алгоритм — общем случае для этого используют алгоритм A*.

A* — это эвристический алгоритм поиска, который итеративно исследует рабочее пространство. Производительность A* сильно зависит от эвристической функции, заданной в качестве входных данных для алгоритма. Эта функция оценивает расстояние до целевого узла (ноды) и используется для фокусировки поиска на цели.

Для графов-сеток сегодня придумано несколько популярных эвристик, таких, например, как Octile Distance. Эта эвристика не только гарантирует отыскания решения, но и то, что оно будет оптимальным. Но основным недостатком использования эвристики Octile Distance или ей подобных является то, что они не учитывают препятствия. Это означает, что в средах с большим количеством препятствий A* может страдать от плохой производительности из-за рассмотрения большого количества лишних состояний в пространстве поиска. Наиболее желанным является достижение идеальной эвристики, которая для каждой клетки графа знает точную стоимость кратчайшего пути до цели, включающего обход всех препятствий.

Чтобы добиться этого и получить учитывающие препятствия эвристики, наиболее близкие к идеальным, группа исследователей из ФИЦ ИУ РАН и AIRI (Даниил Кирилленко, Антон Андрейчук, Александр Панов и Константин Яковлев) использовали передовые методы машинного обучения. Используя трансформерные нейронные сети, команда решила предсказывать два типа эвристических функций.

Первый тип эвристики — это коэффициент коррекции (correction factor, CF), который определяется как отношение между заданной и идеальной эвристическими функциями. Преимущество использования этого коэффициента заключается в том, что он содержит в себе информацию сразу об обеих функциях.

Второй тип эвристики — это карта вероятности пути (path probability map, PPM). Она показывает то, насколько вероятно, что та или иная нода лежит на кратчайшем пути до цели. Эта эвристика может быть использована в рамках фреймворка Focal Search в качестве вторичной. Это позволяет гарантировать, что найденный путь окажется в границах субоптимальности решения.

Архитектура модели, которую ученые используют для предсказания предложенных эвристик, имеет три основных блока: сверточный энкодер, трансформерный блок и сверточный декодер. Свёрточный энкодер состоит из трех ResNet-блоков с даунсэмплингом и направлен на извлечение локальных особенностей экземпляра поиска пути, таких как углы препятствий, узкие проходы и т. д. Свёрточный декодер организован похожим образом, но содержит блоки с апсэмплированием. Наконец, трансформерный блок состоит из четырех комбинаций self-attention-слоя и fit-forward-слоя. Его задача — установить глобальные отношения между особенностями.

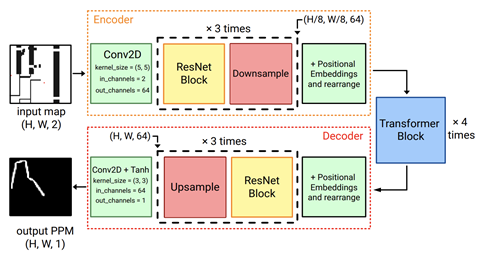
Нейросеть довольно мала и включает всего 1 миллион параметров. Команда обучала каждую модель, используя прямое обучение с учителем с использованием среднеквадратичной ошибки в качестве сигнала обучения.

Авторы провели тщательную эмпирическую оценку на обширном наборе задач планирования. Эксперименты показали, что предложенный подход в ряде случаев четырехкратно уменьшает вычислительные затраты A*, при этом стоимость решения возрастает не более, чем на 0,3% в среднем. При этом он превосходит традиционные методы эвристического поиска, такие как взвешенный A* (WA*), а также предложенные недавно подходы с машинным обучением. Последние включают планировщик от Такахаси с коллегами (A*+HL), который пытается предсказать идеальную эвристику стоимости до цели, и планировщик от Ёнэтани с коллегами (Neural A*), который использует дифференцируемую версию A* для предсказания стоимости определенных шагов.

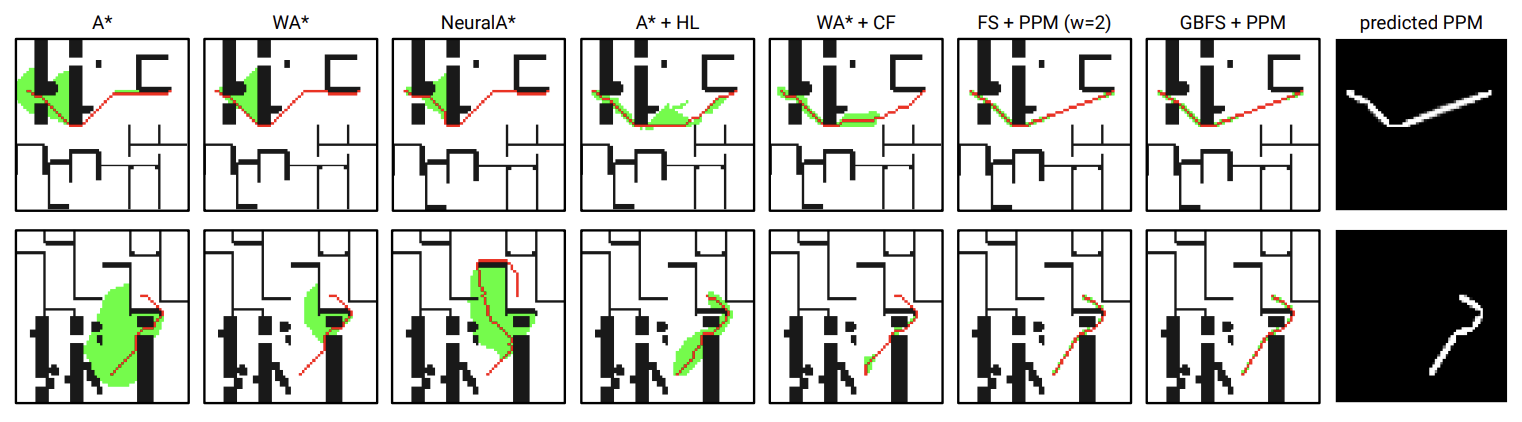
Несколько примеров результатов поиска пути. Раскрытые ноды показаны зеленым цветом, а сам путь — красным. Последний столбец показывает предсказанные PPM.

В будущем команда надеется расширить свои исследования планированием в 3D, планированием с кинодинамическими ограничениями (включая планирование на основе случайного сэмплирования) и еще рядом задач.