Александр Тюрин
Александр Тюрин

Новые алгоритмы ускорят распределённое машинное обучение
Объёмы актуальных вычислительный задач в науке и технике в последние годы часто превышают возможности, которыми может обладать даже очень мощный компьютер. Решением этой проблемы стали распределённые вычисления, в рамках которых компьютеры считают сообща, объединенные в рамках той или иной архитектуры.
Этот принцип в полной мере применим в машинном обучении. Передовые модели требуют для своего обучения и инференса работы сразу нескольких дата-центров, которые могут отличаться оборудованием, конфигурациями, программным обеспечением и ещё рядом условий, а также быть разнесены на существенные расстояния исходя из соображений энергопотребления. В результате некоторые клиенты сети могут выполнять вычисления быстрее, в то время как другие испытывают задержки или даже вообще не участвуют в обучении, что оставляет простор для оптимизации.
Методы математической оптимизации начали развиваться примерно тогда же, когда появилась первая вычислительная техника. Их применение к той или иной области должно учитывать конкретный вид целевой функции. В случае распределённого машинного обучения речь идёт о вычислении функции потерь, что относится к задаче конечномерной невыпуклой оптимизации.
В синхронных методах на основе стохастического градиентного спуска (Stochastic Gradient Descent, SGD) вроде Minibatch SGD вычисления идут со скоростью самого медленного узла, что снижает общую эффективность алгоритма. Поэтому актуально создавать алгоритмы, позволяющие узлам работать асинхронно, то есть независимо друг от друга, без необходимости синхронизации на каждом шаге, и гетерогенно, то есть с различным временем выполнения.
На это направила свои усилия команда учёных из AIRI и Научно-технологического университета имени короля Абдаллы (KAUST). Они не только разработали несколько новых алгоритмов, но и исследовали их теоретическую оптимальность и эффективность. Учёные также доказали новые нижние границы временной сложности для децентрализованной асинхронной оптимизации.
Метод Fragile SGD не требует синхронности и автоматически игнорирует узлы, которые работают слишком медленно или находятся слишком далеко от центрального узла. Он использует остовные деревья для организации коммуникаций между узлами, что позволяет минимизировать время передачи данных. Fragile SGD достигает почти оптимальной временной сложности, которая близка к доказанным нижним границам.
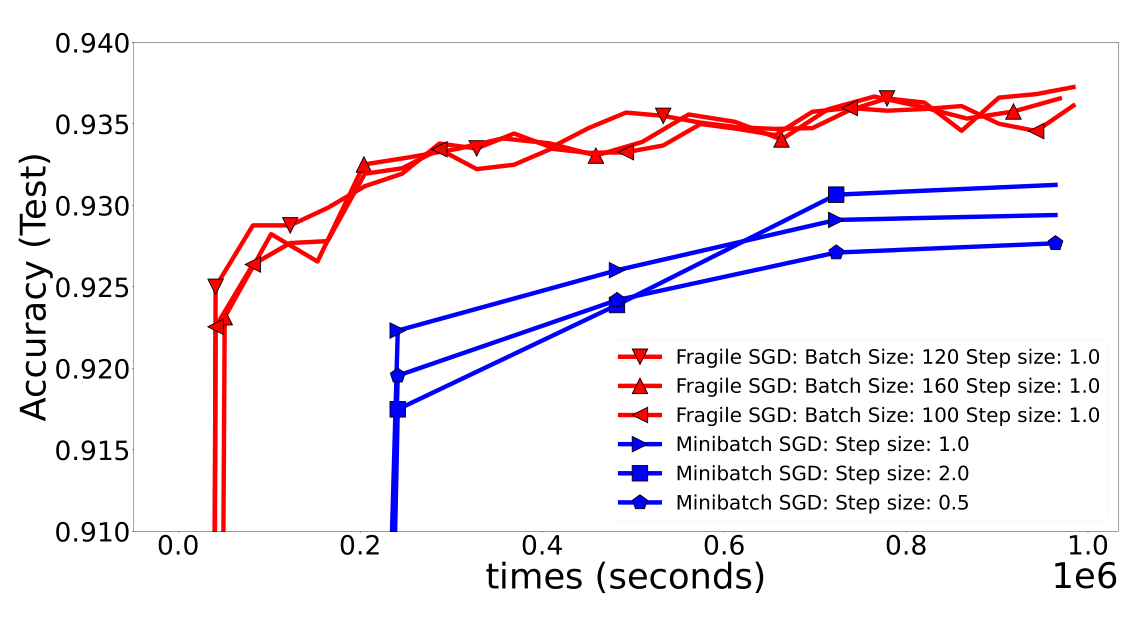
Сравнение точности Fragile SGD и Minibatch SGD на двумерном графе при медленной коммуникации
Amelie SGD заточен под гетерогенные условия, где каждый узел может иметь свой собственный датасет, что характерно для федеративного обучения. Авторы доказали его оптимальность.
Одной из ключевых идей метода Shadowheart SGD стало использование нового математического аппарата, основанного на равновесном времени. Оно определяет оптимальное время, которое каждый узел должен потратить на вычисления и коммуникации, и определяется параметрами системы. Другой особенностью Shadowheart SGD является использование несмещённого сжатия данных, что позволяет уменьшить объём передаваемых данных без значительного увеличения ошибки.
Наконец, метод Freya PAGE хорошо подходит для задач с эмпирическим риском и опирается на совершенно новые стратегии сбора стохастических градиентов: ComputeGradient и ComputeBatchDifference. Авторы показали, что Freya PAGE имеет оптимальную временную сложность в условиях, когда количество данных значительно больше числа устройств.
Все описанные методы способны адаптироваться к изменяющимся условиям вычислений, что особенно полезно в реальных системах, где производительность устройств может меняться со временем. Авторы представили их на конференции NeurIPS 2024 в трёх научных статья (1, 2, 3).