Общая ковариантность помогла нейросетям точнее решать дифференциальные уравнения

Обширные явления реального мира, такие как турбулентность, атмосферная циркуляция и напряжение деформируемых материалов и т.д., описываются лежащими в их основе дифференциальными уравнениями в частных производных (Partial differential equations, PDEs). Следовательно, решение PDEs является общей фундаментальной проблемой для многих научных и инженерных областей и может принести дальнейшую пользу важным приложениям реального мира. Например, моделирование воздушного потока для проектирования аэродинамического профиля крыла летательного аппарата, моделирование атмосферы для прогнозирования погоды, молекулярная динамика и т.д.

Традиционный подход к численному решению PDEs основан на использовании различных численных солверов, которые используют те или иные классические методы. Например, метод конечных элементов (FEM), метод конечных разностей (FDM), которые решают PDEs путем дискретизации расчетной области. Однако, в этом случае точность численного решения сильно зависит от дискретизации расчетной сетки: грубые сетки работают быстро, но менее точно; мелкие — точны, но медленны. В реальных приложениях решение PDEs обычно требует очень хорошей дискретизации и, следовательно, очень сложны, времязатратны и трудоемки для традиционных солверов.

В последние несколько лет на решение этой проблемы направлены усилия ученых, занимающихся нейронными сетями (NNs). Широко известно, что NNs являются универсальными аппроксиматорами непрерывных функций. Более важным фактом является то, что NN с одним скрытым слоем может точно аппроксимировать любой нелинейный непрерывный оператор. Недавно в рамках нового направления было предложено изучение бесконечномерных операторов с помощью NNs. Нейронный оператор устраняет зависящую от сетки дискретизацию, создавая единый набор параметров NN, которые можно использовать с различными дискретизациями расчетной сетки. В этом случае мы имеем возможность передавать решения между расчетными сетками. Кроме того, нейронный оператор нужно обучить только один раз. Наконец, нейронный оператор не требует знания, лежащего в основе PDE, — только данные, полученные с помощью солверов или экспериментально.

Трудности решения PDEs с помощью нейронных операторов

Такой подход получает решение довольно быстро, но трудность заключается в том, что, чтобы получить хорошую точность, обучающих пар наблюдений должно быть много. Другими словами, мы опять упираемся в дороговизну таких вычислений. В классическом машинном обучении было предложено несколько способов, целью которых было увеличить количество данных для обучения без существенных вычислительных затрат. Однако, для задач, связанных с PDEs, методов увеличения данных без существенных вычислительных затрат очень мало. Команда ученых из Сколтеха, ИВМ РАН и AIRI под руководством Ивана Оселедца разработала новый метод, позволяющий увеличивать набор данных для обучения нейронного оператора.

Центральной идеей предложенного подхода является принцип общей ковариантности. Он заключается в том, что физика явления не зависит от выбора системы координат. Математически, ковариантность означает, что физические поля являются геометрическими объектами с определенными законами преобразования при изменении системы координат.

В ряде случаев такие преобразования оставляют инвариантными уравнения, но в большинстве случаев сохраняется только форма уравнения. Более точно, для PDEs преобразование координат, выбранное соответствующим образом, приводит к изменению параметров задачи (например, поля проницаемости, коэффициента конвекции, начальных или граничных условий и т.д.). Ученые использовали этот факт для построения вычислительно дешевой и широко применяемой стратегии увеличения данных (аугментации), основанной на простых случайных преобразованиях системы координат.

Новые данные за счет преобразования координат

Традиционный подход к численному решению дифференциальных уравнений основан на представлении искомого решения в виде кусочно-линейной интерполяции по области определения. В слабой форме он эквивалентен задаче о решении системы линейных уравнений на коэффициенты интерполяции. С точки зрения машинного обучения признаками в данном случае могут служить значения известных функций в точках интерполяционной сетки, а целевыми параметрами — коэффициенты для искомой функции.

С другой стороны, если мы преобразуем аргументы с помощью некоторой аналитической и строго монотонной функции, то форма уравнения не поменяется. Подобные преобразования можно вывести с помощью кумулятивных функций распределения со строго положительной плотностью вероятности (например, на основе тригонометрических рядов). Это означает, что мы можем переопределить признаки и целевые данные, просто отталкиваясь от уже известных пар «входные данные — решение». Единственное, что нужно сделать, это провести их корректировку в соответствии с законом преобразования для дифференциального уравнения.

Проверка на практике

Предложенная аугментация универсальна и может быть использована для любого нейронного оператора. Ученые продемонстрировали этот подход на примере решения уравнения переноса, волнового уравнения, уравнения Навье — Стокса и эллиптических уравнений двух типов. В их исследовании использовались следующие нейронные операторы: FNO, SNO, MLP, DilResNet, DeepONet и U-Net. Эксперименты проводились для уравнений от одной и двух переменных.

Проверка показала, что предложенная аугментация позволяет ощутимо снизить ошибку обученного нейронного оператора при тестировании. Наименьшее снижение наблюдалось при работе с MLP — ошибка снизилась на 17%. Наилучший же результат был достигнут при работе с сетью DilResNet — там этот показатель вырос до 80%. В среднем по нейронным операторам и уравнениям предложенный подход сократил ошибку тестирования на 23%.

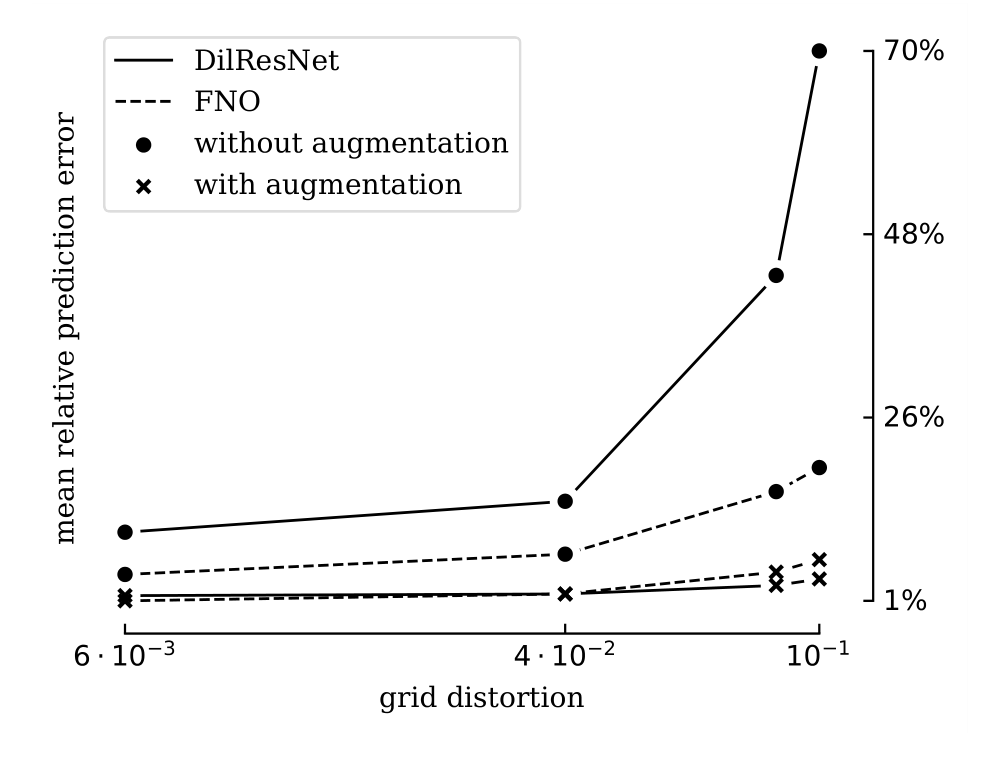
Зависимость ошибки предсказания от возмущения решетки (grid distortion) при решении с помощью FNO и DilResNet с применением предложенной аугментации и без нее