Ученые сделали разложение в тензорный поезд быстрее и точнее

habr 280623-2.png

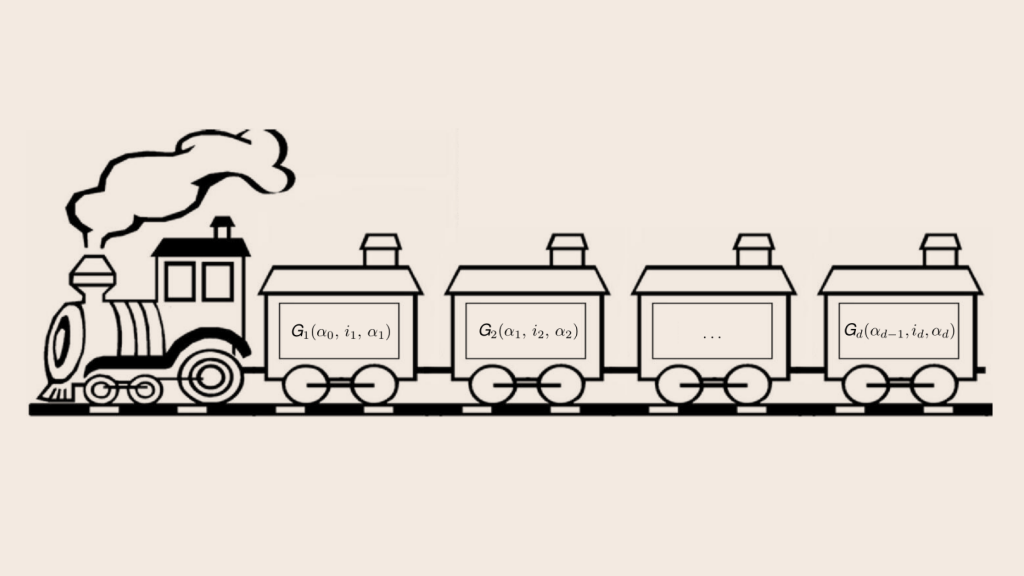
Коллаж AIRI. Источник: iclcollective.com

Машинное обучение, как и некоторые другие виды статистических задач, страдают от проблемы, которая получила емкое название «Проклятие размерности». Она возникает в тот момент, когда число признаков в модели становится слишком большим — количество данных растет экспоненциально с размерностью пространства, что не только повышает трудоемкость вычислений и требует ресурсы на хранение, но и ставит под угрозу успешность обучения.

Тензорные поезда

Одним из способов борьбы с этой проблемой стал алгоритм, основанный на разложении тензоров с большой размерностью (в данном случае многомерных массивов комплексных чисел) в тензорный поезд (tensor train, TT). Первым его описал Иван Оселедец, работающий ныне в Сколтехе и AIRI. В рамках этого подхода тензор большой размерности может быть представлен через произведение нескольких тензоров малой размерности (ядер разложения), которые суммируются по общим индексам. Во множестве важных задач этот подход позволяет многократно уменьшить количество ячеек памяти, необходимых для работы.

Существующие методы, например, крестовая TT-аппроксимация или чередующийся метод наименьших квадратов, рассматривают тензор как черный ящик. Другими словами, они игнорируют возможную аналитическую связь между компонентами тензора и их индексами. Из-за этого существующие методы имеют большое время работы и плохую сходимость, даже если точное решение известно.

Аналитическая зависимость от индексов

Чтобы задействовать этот ресурс Иван Оселедец совместно с научным сотрудником Сколтеха Глебом Рыжаковым предложили новый метод построения ядер ТТ-разложения, который учитывает аналитическую зависимость компонент тензора от индексов. Технически это реализовано через цепочку функций, которые получили название производящих. Каждая из них зависит от индекса тензора, а также от результата применения другой функции на предыдущем шаге.

К сожалению, не существует единого алгоритмического подхода для построения последовательности производящих функций по заданной аналитической зависимости значения тензора от его индексов. Более того, такое представление не единственно, и разные представления могут привести к разным рангам результирующего тензора. Ученые проиллюстрировали этот факт несколькими примерами различных наборов производящих функций для одного и того же тензора. Однако оказывается, что существуют достаточно общие закономерности для производящих функций, и на основе приводимых примеров несложно строить нужные последовательности по аналогии.

Предложенный подход работает лучше всего в тех случаях, когда производящие функции вместе с самим тензором имеют небольшое количество возможных значений. При этом ТТ-ядра, полученные новым методом, сильно разрежены, что дает дополнительный выигрыш в производительности.

Проверка на практике

Авторы убедились в этом, применив алгоритм к ряду задач, включающему в себя кооперативные игры, задачу о рюкзаке, задачу о n ферзях, вычисления перманента матрицы и многое другое. Так, в кооперативных играх новый подход показал превосходство, как по времени выполнения, так и по точности по сравнению с существующими методами. В случае же с вычислением перманента оценочное число операций оказалось всего в два раза больше, чем в оптимизированном ad hoc методе на основе гамильтоновых блужданий. Важно, что предложенный подход не только решает проблему проклятия размерности, но и реализует алгебру для TT-тензоров.

Сравнение времени в секундах (сверху) и относительной точности (снизу) для четырех кооперативных игр для нового метода (зеленый цвет), метода кросс-аппроксимации, предложенным Баллестер-Риполлом (оранжевый цвет), и прямого суммирования (синий цвет)

Ученые отмечают, что недостатком нового метода является быстрый рост рангов ядер в случае, если размер множества образов, которым обладают производящие функции, слишком велик. Несмотря на то, что эту проблему можно решить с помощью специальной процедуры ограничения рангов, авторы планируют расширить свой алгоритм и на такой случай.

Подробнее с работой можно ознакомиться в статье, опубликованной в сборнике трудов конференции ICLR2023.