Марат Хамадеев
Марат Хамадеев

Тензорный поезд сделал безградиентную оптимизацию эффективнее
Оптимизация — это задача, которая лежит в основе множества алгоритмов машинного обучения. Обычно она сводится к нахождению минимума или максимума некоторой функции множества переменных. Одним из первых подходов к решению данной задачи стал градиентный спуск. Он заключается в движении от некоторой точки многомерной поверхности, образованной функцией, в сторону её убывания, направление которой указывает градиент, взятый с обратным знаком.
Несмотря на то, что градиентный спуск был предложен ещё в XIX веке, он до сих пор остаётся крайне популярным методом в машинном обучении и работе данными благодаря своей простоте. Вместе с тем, метод становится вычислительно сложным, когда требуется оптимизировать модель с большим числом параметров, чреват застреванием в локальных минимумах, а в ряде случаев градиент вообще невозможно рассчитать.
По этой причине учёные активно развивают методы безградиентной оптимизации на основе иных математических принципов. Одно из направлений исследований опирается на дискретизацию функций и поиск минимального или максимального элемента в неявно заданном многомерном массиве (тензоре). Большую роль здесь играют методы разложения тензоров с большой размерностью в тензорный поезд (tensor train, TT), то есть представление их через произведение нескольких тензоров малой размерности, что помогает преодолеть «проклятие размерности». Такие подходы как TTOpt и Optima-TT, а также их модификации уже показали свою работоспособность в задаче безградиентной оптимизации, поэтому эта область исследований постоянно развивается.
Ранее мы уже рассказывали, как команда исследователей из AIRI и Сколтеха под руководством Ивана Оселедца сделала разложение в тензорный поезд быстрее и точнее. На этот раз учёные использовали такое разложение для решения задачи безградиентной оптимизации многомерной функции типа чёрного ящика. Особенной этой задачи в том, что у исследователей нет никакой информации об устройстве такого чёрного ящика, включая даже то, дифференцируема ли эта функция, а большая размерность затрудняет использование традиционных методов. Подобные ситуации всё чаще встречаются в областях, которые сталкиваются с Big Data.
Новый метод основан на выборке нескольких векторов из некоторого тензора (тензора вероятности), представленного в TT-формате. Эти векторы подаются на вход чёрного ящика, который вычисляет для них значение функции, после чего специальный алгоритм по определенному критерию выделяет из выходных значений поднабор кандидатов. Эти кандидаты служат для обновления исходного тензора с помощью минимизации loss-функции, составленной как сумма логарифмов вероятностей в отобранных точках. По этой причине метод получил название вероятностной оптимизации с тензорной выборкой (Probabilistic Optimization with Tensor Sampling, PROTES).
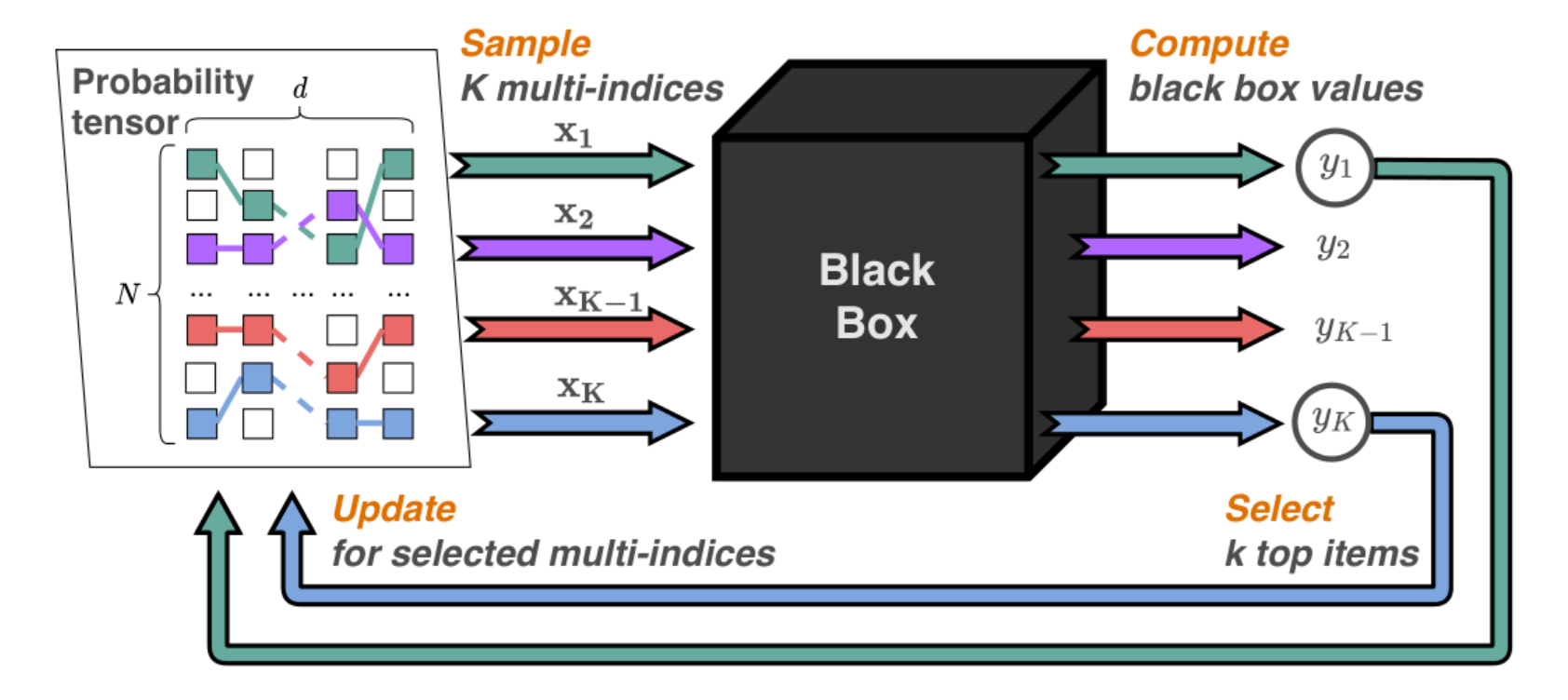
Схема оптимизации черного ящика с помощью алгоритма PROTES
Авторы протестировали новых подход на 20 модельных задачах, включающих квадратичную бинарную оптимизацию и оптимальный контроль. Результаты сравнивались с 7 популярными методами оптимизации, как классическими, так и более современными и также основанными на тензорном разложении. Эксперименты показали, что PROTES демонстрирует преимущество в подавляющем большинстве задач.
На данном этапе наш метод скорее эвристический. Мы пока больше фокусировались на возможности его практического приложения к достаточно разным и интересным задачам, нежели на строгом теоретическом обосновании. Оценки сходимости, рангов, числа операций и многое другое нам ещё предстоит сделать в будущем.

Программный код предлагаемого метода и численные примеры доступны в публичном репозитории, детали исследования можно найти в статье, опубликованной в сборнике трудов конференции NeurIPS 2023.