Марат Хамадеев
Марат Хамадеев

Звёздообразная архитектура улучшит генерацию с помощью диффузионных моделей
Если отрыть флакон с духами, то вскоре летучие молекулы парфюма равномерно заполнят комнату благодаря процессу диффузии. Точно также осмысленная структура данных, которая в течение некоторого времени подвергается размытию, постепенно превращается в шум. Но даже если размытие описывается аналитическим распределением, его непосредственная инверсия — то есть, фактически, удаление шума — становится вычислительно неподъёмной.
На помощь в данной ситуации могут прийти нейронные сети. Их можно обучить, подавая на вход большую выборку, характеризующую процесс размытия данных. Такие выборки состоят из пар данных, первые из которых являются информативными, а вторые получены из первых за несколько итераций размытия. Обученные таким образом модели называются диффузионными или, если более полно, диффузионно-вероятностными моделями с шумоподавлением (denoising diffusion probabilistic models, DDPM). Они способны не только эффективно удалять шумы из изображений или звуков, но и рисовать довольно реалистичные картины и иллюстрации.
Процесс размытия данных традиционно опирается на гауссово распределение, подобно тому, как диффундируют молекулы газа. Оно позволяет свести задачу к цепям Маркова, в которых состояние на каждом этапе, описываемое некоторым маргинальным распределением, зависит только от состояния на предыдущем шаге. Проблема в том, что этот подход релевантен только для определенного типа данных, например, изображений, в то время как для данных на многообразиях с ограничениями, таких как единичная сфера или положительные полуопределенные матрицы, или данных с иными особенностями впрыскивание гауссового шума будет противоестественным. В ряде частных случаев удаётся приспособить другие распределения, например, категориальные и гамма распределения, но общего решения данной проблемы пока нет.
На борьбу с этой трудностью свои усилия направил коллектив учёных из Европы и России под руководством Дмитрия Ветрова. В основе их идеи лежит отказ от марковской архитектуры алгоритма. Вместо него исследователи предложили подход, в котором маргинальное распределение каждого шага всё еще остаётся связанным с начальным распределением по мере его превращения данных в шум. Если представить марковскую цепь как последовательность шагов, то новый подход будет скорее напоминать звезду. По этой причине авторы назвали его звездообразной (Star-Shaped, SS) DDPM.
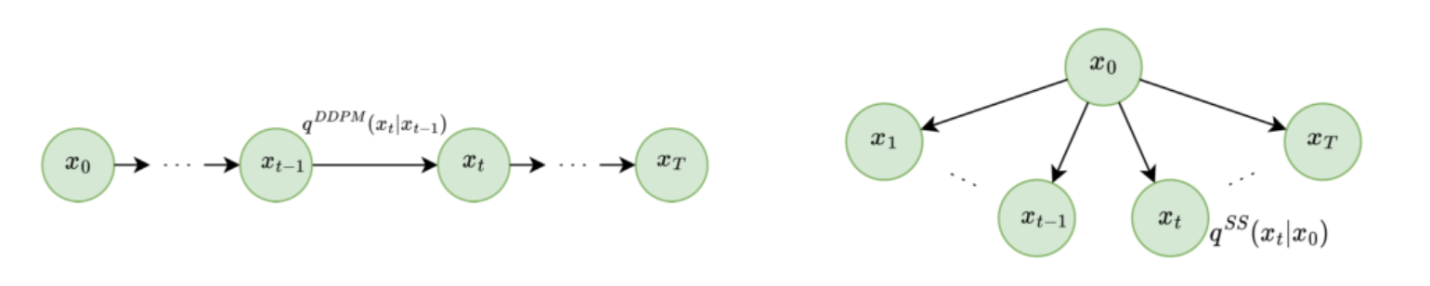
Слева: марковский процесс прямой диффузии в традиционной DDPM. Справа: аналогичный процесс в SS-DDPM.
Важное преимущество, которое предоставляет SS-DDPM — это выход за рамки гауссовых распределений и расширение их класса до экспоненциального семейства. Авторы убедились в этом для некоторых из них, в частности, распределений фон Мизеса – Фишера, Дирихле, Уишарта, а также бета-распределения. При этом модель оказывается эквивалентной DDPM, если использовать привычное распределение Гаусса.
Чтобы оценить, как внедрение звёздообразной архитектуры влияет на эффективность решения задачи, исследователи провели ряд экспериментов. Проверка включала работу с синтетическими данными, сгенерированными на симплексах и многообразиях положительных полуопределенных матриц, геодезическими данными (пожары на поверхности Земли), категориальными данными (тексты), а также изображениями. Во всех случаях модели SS-DDPM имели преимущество, либо были сопоставимыми с базовыми или усовершенствованными методами DDPM.
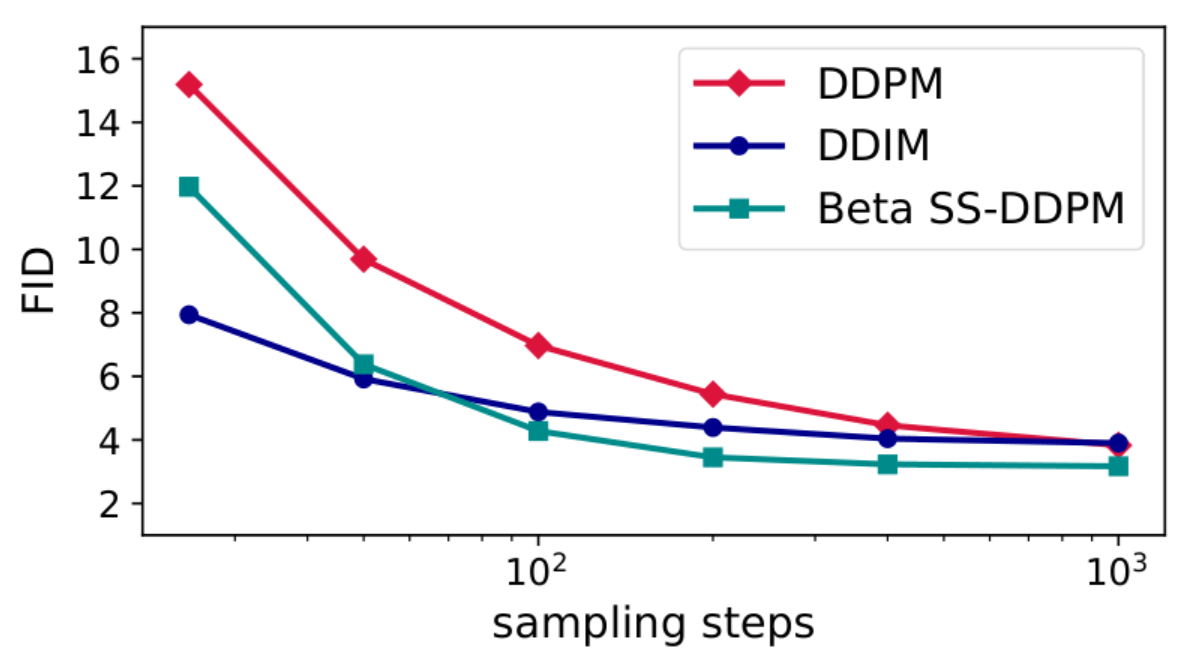
Сравнение SS-DDPM с бета-распределением, обычной DDPM и её усовершенствованной версией DDIM по метрике латентного расстояния Фреше (FID) в задаче генерации изображений
При генерации изображений мы убедились, что звездообразная диффузия c бета-распределенным шумом достигает производительности, сравнимой с гауссовой DDPM. Этот факт свидетельствует о том, что использование гауссового распределения может быть далеко не самым оптимальным, а значит и диффузионные модели ещё можно улучшить. Со своей стороны мы надеемся в будущем найти возможность обобщить SS-DDPM для более широкого класса распределений, нежели экспоненциальное семейство.
Код моделей открыт и доступен на GitHub. С деталями самого исследования можно ознакомится в статье, опубликованной в сборнике трудов конференции NeurIPS 2023.