Scientists made tensor train decomposition faster and more accurate

habr 280623-2.png

Collage AIRI. Credit: iclcollective.com

Machine learning like some other types of statistical problems suffers fr om a problem called “curse of dimensionality”. It arises when number of features of a model becomes too big. The amount of data grows exponentially that not only boosts the laboriousness of calculation and the requirements for the data storage but also jeopardizes learning success.

Tensor trains

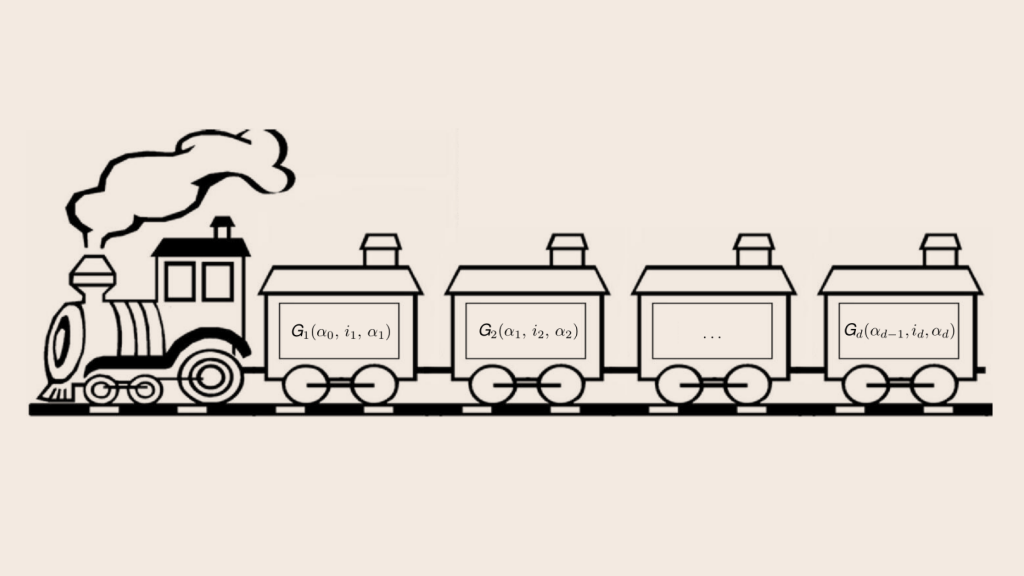
One way to circumvent this problem is an algorithm based on the decomposition of a multidimensional tensor (a multidimensional array of complex numbers) into a tensor train (TT). It has been first proposed by Ivan Oseledets, now a staff member of Skolkovo Institute of Science and Technology and AIRI. In this method, the multidimensional tensor can be expressed in terms of the product of several low-dimensional tensors (TT-cores). In a number of important cases this approach allows one to significantly reduce the number of memory cells required for data processing.

Existing methods like TT-cross approximation method or alternating least squares method are treating the tensor values as a black box. In other words, these methods do not take into account the analytic dependence, if any, of the tensor value on its indices. Because of this, existing methods can build a TT decomposition for a long time and can have poor convergence, even if the original tensor has an exact TT decomposition.

Analytical dependence on indices

To make use of this resource Ivan Oseledets in collaboration with Skoltech research fellow Gleb Ryzhakov have present recently a fast method to directly construct cores of the TT decomposition of a tensor for which the analytical dependence of the tensor value on the values of its indices is known. Technically, the new method works with functions, each of which depends on tensor index and which are sequentially applied to the values of the previous functions. Authors called them derivative functions.

Unfortunately, there is no single algorithmic approach for constructing a sequence of derivative functions based on a given analytical dependence of the tensor value on its indices. Moreover, such a representation is not unique and different representations can lead to different ranks of the resulting tensor. Team gave several examples of different sets of derivative functions for the same tensor. However, it turns out that there are fairly general patterns for derivative functions. Authors hope that, based on the examples they give from various applications of the method, it is easy to construct by analogy the desired sequence of derivative functions for a particular application problem.

It turned out that the new approach works best in cases wh ere the derivative functions together with the tensor itself have a small number of possible values. At the same time, TT-cores, obtained by the new method, are highly sparse, which gives an additional gain in performance.

Practical application

The team proved this applying the algorithm to a range of problems, including cooperative games, the knapsack problem, the n-queen problem, matrix permanent calculation, and more. In cooperative games they have compare it with existing methods and show our superiority both in execution time and in accuracy. For the problem of calculating matrix permanent the new method gives an estimated number of operations only twice as large as the optimized ad hoc method of calculating the permanent using Hamiltonian walks. It is important that proposed approach not only allow to overcome the curse of dimensionality but also implements algebra for TT-tensors.

Times in seconds (top) and relative accuracy as functions of number of players (bottom) for four cooperative games. Blue — calculating the sums directly, orange — results from the paper of Ballester-Ripoll, 2022, green — the new method.

Scientists noticed that the fast growth of the ranks in the case when the derivative functions have a large size of their image set is a limitation of their method. Although they have a rank restriction procedure for this case, authors plan to specify an extension of the algorithm to accurately construct a TT-decomposition for such cases as well, if it is known to be low-ranked.

More details can be found in the article published in the Proceedings of the ICLR 2023 conference.