Marat Khamadeev
Marat Khamadeev

Bulk Search Improved Anonymous Multi-Agent Path Finding
It is difficult to argue with the thesis that soon, many everyday tasks will be performed by robots controlled by various artificial intelligence algorithms. However, there are many obstacles on this path. For example, if there is more than one robot, it is necessary to ensure they do not obstruct each other while moving.
Researchers are already working on ensuring the latter by formalizing this robotics problem using the movement of a set of abstract agents on a graph. The class of problems related to the movement of multiple agents is called Multi-Agent Path Finding (MAPF).
Solving MAPF problems does not require knowledge of the technical device of the agent, although some nuances allow these problems to be divided into several types. For example, if there is a central controller in the system capable of seeing all agents and their goals, as well as coordinating their movements, this problem is called centralized MAPF. From the algorithmic perspective, it is simpler than the decentralized variant where instructions have to be devised for each agent individually, which is why existing algorithms like RHCR and PIBT show quite high efficiency.
Another simplification is Anonymous MAPF (AMAPF) where agents are indistinguishable, and any agent can be directed to any goal. This situation, for example, occurs in automated warehouses. The general approach to AMAPF optimization is based on constructing an auxiliary graph on which the maximum flow problem is solved. However, such a graph, called a network, is often much larger than the original graph, which slows down computations.
This issue was addressed by a team of researchers consisting of Konstantin Yakovlev, a leading researcher at FRC CSC RAS and AIRI, and Zain Alabedeen Ali, a graduate student at MIPT. They hypothesized that one can compress single search states of a graph into bulks that form a sequence and operate with the latter, increasing the algorithm's speed. The method they developed was dubbed Bulk Search (BS).
The team demonstrated that from a mathematical point of view, Bulk Search is complete. To practically validate their innovation, the authors conducted a series of experiments on a popular benchmark proposed by Stern and colleagues and compared the results with the state-of-the-art AMAPF solver described by Okumura and Defago. The benchmark consists of 33 maps of different sizes and 25 random scenarios of agents and goals placement. The Okumura and Defago’s solver, in turn, addresses the issue of multiple states using the Ford-Fulkerson algorithm.
First, researchers compared the goal achievement percentage (success rate) for both algorithms under the condition that the time for the last agent to reach the end was limited to 30 seconds. The experiment showed that the BS approach succeeded in 100 percent of cases, while its predecessor lost efficiency as the map size increased.
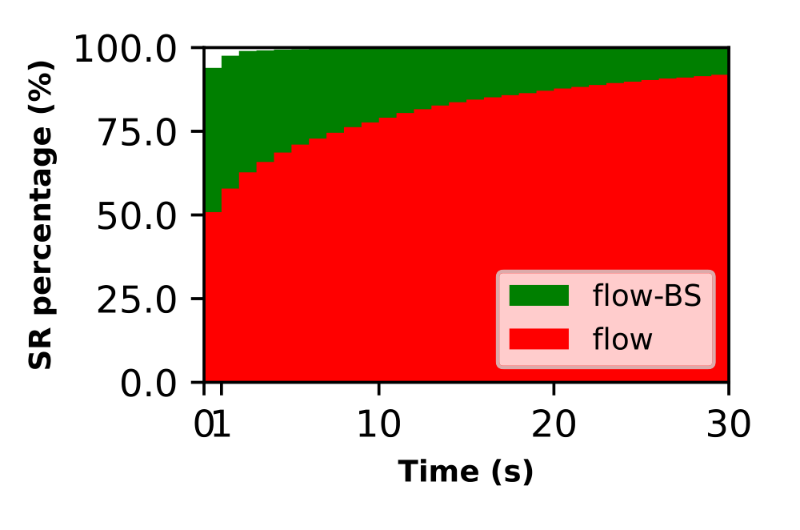
The (normalized) number of instances solved by a certain time cap
In the second stage, the authors studied how the number of agents on the map affects the algorithm's performance. They found that the BS approach reveals significantly fewer nodes, which explains its speed. In the future, scientists plan to extend the proposed search technique to support costs (e.g. Min-Cost-Maximum-Flow) to solve other MAPF problems.
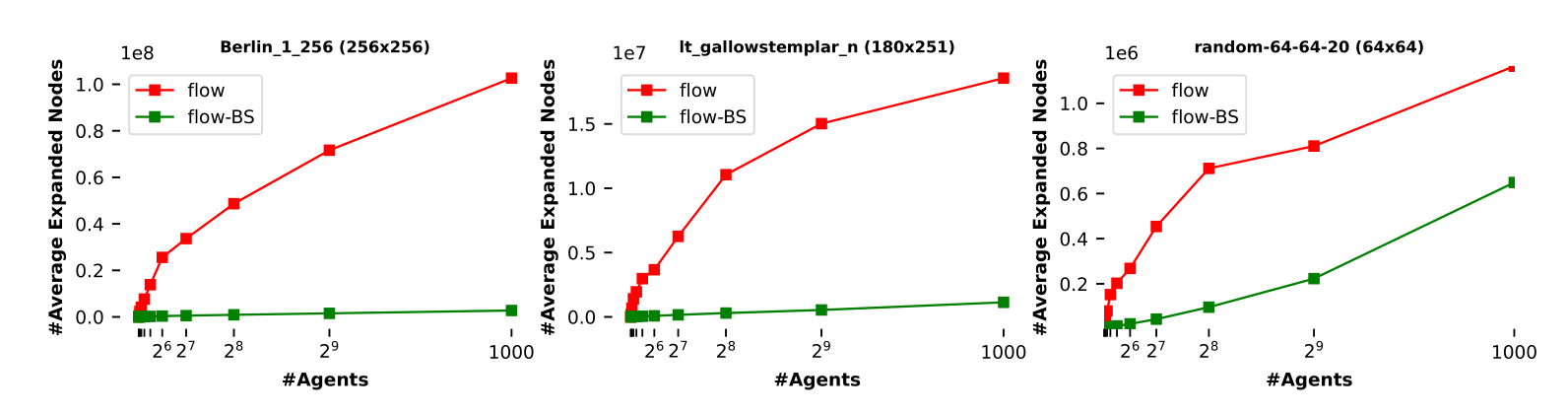
The number of expanded nodes with a different number of agents on different maps
The research was presented at the AAAI-24 conference, and the corresponding article was included in the proceedings, with the code available in the GitHub repository. At the same conference, a team of researchers, including Konstantin Yakovlev, reported on successes in improving decentralized MAPF methods under limited visibility conditions. Recently, we briefly summarized their work.