Milena Gazdieva
Milena Gazdieva

Unbalanced optimal transport helped to make the barycenter estimation robust
In machine learning, the problem of aggregation often arises — combining data originating from multiple sources. For example, these could be brain MRI images taken on different scanners. It is important to reduce the particular source-specific characteristics and leave only source-agnostic information during the aggregation.
The framework of the Optimal Transport (OT) barycenter has proven effective in solving aggregation problems. Optimal Transport refers to the task of efficiently transitioning from one probability distribution to another. The concept of barycenter arises when it is necessary to discover a geometrically meaningful average of these distributions by minimizing the average OT costs from the reference distributions to the desired one.
In recent years, there has been significant progress in developing methods for computing OT barycenters, allowing them to be adapted to high-dimensional data setups, e.g., images. However, current barycenter research tends to ignore a typical and important property of data appearing in real-world applications: the presence of undesirable noise and outliers.
This shortcoming was noted by a team of researchers from AIRI and Skoltech, along with colleagues from the Georgia Institute of Technology and Sungkyunkwan University. To find a robust approach based on OT barycenters that inherit all advancements in this field, they turned to continuous unbalanced OT techniques which are naturally aligned with data imperfection.
In classical optimal transport, the marginals (individual distributions) of the OT plan coincide with the original and target distributions. The idea of unbalanced OT relies on softening such correspondence, allowing for more flexibility in dealing with noise and outliers. The authors of the study focused on semi-unbalanced optimal transport (SUOT), where the marginal does not coincide with the initial distribution.
The essence of the new work lies in developing an approach for estimating the barycenter of continuous distributions in terms of the SUOT distance. The researchers theoretically demonstrated that this problem can be reduced to a minimax problem of finding a saddle point and proposed using neural networks to solve it.
The authors conducted a series of experiments with several popular datasets, including the colored MNIST. In the latter case, the scientists worked in the latent space of a StyleGAN model, which had been pre-trained on a dataset of red and green digits "2" and "3." They added a small percentage of white color as an outlier and also considered a digit dataset ("2," "3"), adding a small percentage of digit "7".
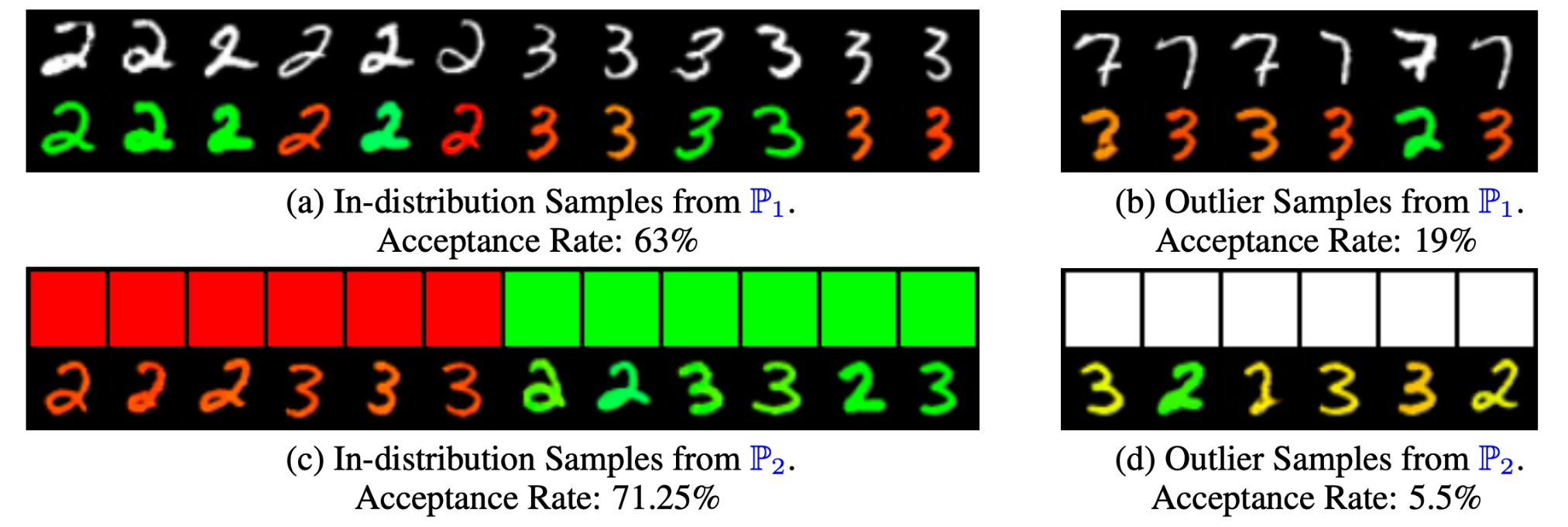
Acceptance rates for different numbers and colors obtained during the experiment. On the right are the results for outliers.
The researchers showed that the SUOT approach to finding barycenters effectively ignores outliers during the inference stage. According to them, the proposed method opens up new opportunities for scalable computations and applications in a wide range of tasks where reliable averaging of complex probability distributions is required.
The paper describing the method and experiments was accepted at the ICLR 2025 conference and published in its proceedings.