Marat Khamadeev
Marat Khamadeev

General covariance helped neural networks to solve differential equations more precisely
Differential equations play an important role in many sciences, such as in physics. In most problems scientists and engineers deal with every day its solution can only be found numerically. This is especially true if one deals with partial differential equation (PDE) containing an unknown function of many variables and its partial derivatives.
A traditional approach to solve them numerically is based on solvers which use various methods (for example, finite-element method). Result of their work is unique and well interpretable. However, the accuracy with which the numerical solution reproduces the analytical one depends strongly on the number of elements involved which ultimately depends on the computational capabilities. Thus, numerical calculations are very expensive.
Machine learning is increasingly used to solve PDEs. The especially fruitful idea is to learn
a computationally cheap but sufficiently accurate surrogate for the classical solver. The most reliable training strategy is to generate input-output pairs with a classical solver and fit a neural network of choice with a standard L2
loss (regression setting).
Neural PDE solvers meet problems
In the regression setting the size of the generated dataset is usually limited owing to the restrictions on the computation budget. Deep learning is data-hungry, so ways to cheaply increase the number of data points available for training are highly desirable. Numerous augmentation techniques serve this purpose in classical machine learning. For scientific machine learning, literature on augmentation is scarce. In this note, a research team from Skoltech, INM RAS and AIRI led by Ivan Oseledets contributed a new way to augment datasets for neural PDE solvers.
The central idea behind the new approach is the principle of general covariance. General covariance states that physical phenomena do not depend on the choice of a coordinate system. Mathematically, the covariance means the physical fields are geometric objects (tensors) with particular transformation laws under the change of coordinates. In exceptional cases, these transformation laws leave governing equations invariant (symmetry transformation), but in most cases, it is only the form of the equations that persists. More specifically, for parametric partial differential equations, suitably chosen coordinate transformation induces the change of problem data (e.g., permeability field, convection coefficients, source term, initial or boundary conditions, e.t.c.). Scientists used this fact to build a computationally cheap and broadly applicable augmentation strategy based on simple random coordinate transformations.
Novel solutions from coordinate transformations
The usual way to approximate the solution of a differential equation is to use finite-element discretization, i.e., to interpolate it with a set of piecewise linear functions. In a weak form the task is equivalent to solving a system of linear equations on interpolation coefficients. For machine learning approach one can generate a dataset with features and targets taking all the functions at the points of the interpolation grid.
On the other hand, if one transforms the coordinates using an analytic strictly monotonic function the transformed equation has the same parametric form as the original one. Such transformations can be derived from cumulative distribution functions with strictly positive probability density (for example, basen on trigonometric series). After that one can redefine features and targets and generate novel solutions from the old ones using smooth coordinate transformations and interpolation. The only thing left to do it to adjust interpolated features and targets according to the transformations law for PDE evaluated in new coordinates.
Practical test
Proposed augmentation is easily extendable and architecture-agnostic. To evaluate its efficiency, the team performed empirical tests on the two-way wave, convection-diffusion, and stationary diffusion equations using several variants of neural operators: FNO, SNO, MLP, DilResNet, DeepONet и U-Net.
For tried neural networks and partial differential equations, proposed augmentation improves test error by 23% on average. The worst observed result is a 17% increase in test error for multilayer perceptron, and the best case is a 80% decrease for dilated residual network.
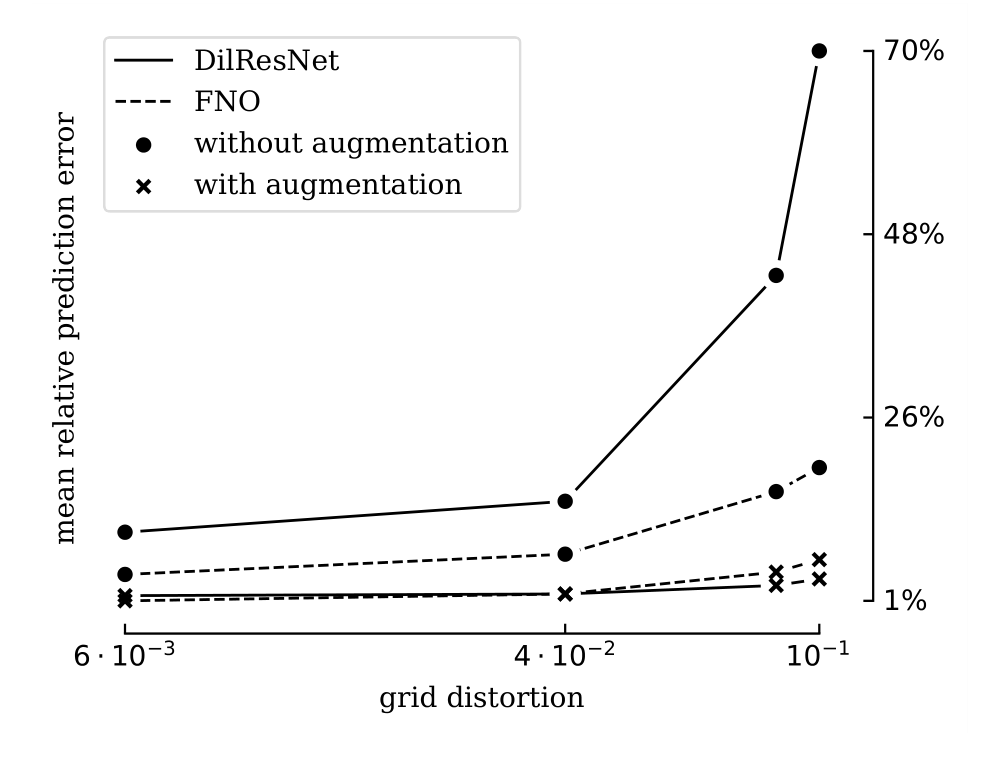
Sensitivity to grid distortion for DilResNet and FNO with and without augmentation
One of the limitations of our approach is the fact that the augmentation of this type is applicable to a small set of equations. In the future, we plann to expand the range of its applicability by considering more complex equations and unstructured grids

More details can be found in the article published in the Proceedings of the ICML 2023 conference.