Marat Khamadeev
Marat Khamadeev

Using the general cost functional made the optimal transport with class preservation more accurate
In the mid-20th century, Soviet mathematician Leonid Kantorovich developed ideas for optimal solutions in economics, including the problem of optimal cargo transportation. Today, his work forms the basis of optimal transport (OT) models, where probabilistic distributions have replaced resource distributions for drawing images in generative neural networks.
We have previously discussed the successes achieved by the "Learning Intelligence" team at AIRI, led by Evgeny Burnaev, in this area. For example, not long ago, researchers presented the transportation problem as the search for a saddle point of a functional. This made optimal transport scalable and theoretically grounded.
Recently, the group turned its attention to the fact that continuous OT methods typically rely on various Euclidean distances, such as l1 or l2, traditionally used in optimization problems. Despite their simplicity and prevalence, choosing such costs for problems where a specific optimality of the mapping is required may be challenging. For example, when one needs to preserve the object class during the transport the Euclidean function may be suboptimal.
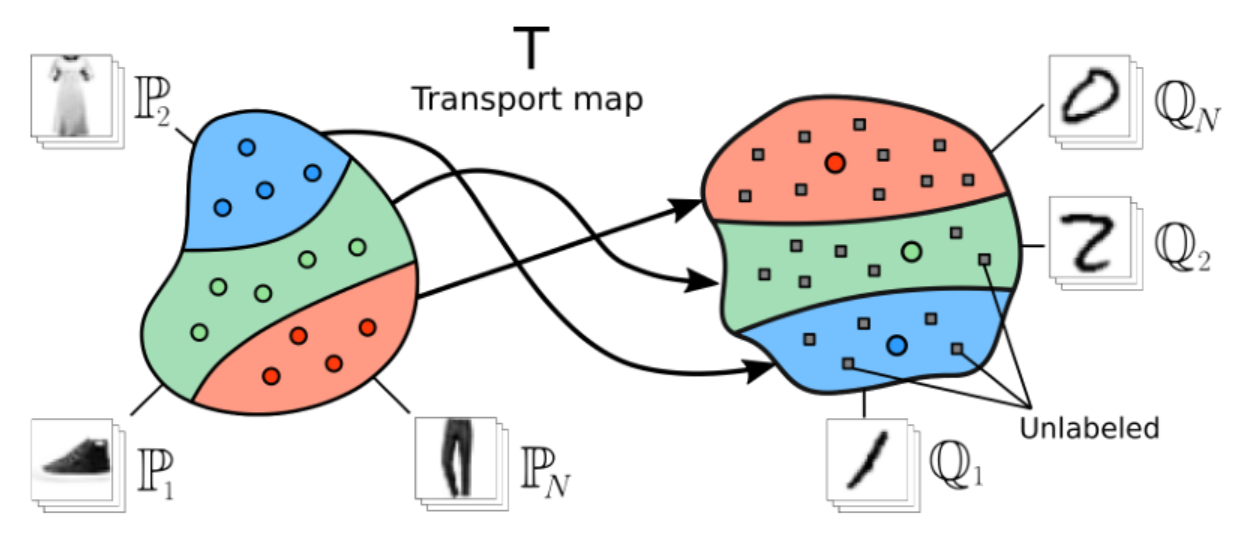
An illustration of the transport problem, where it is required to preserve the class of objects when transferring from one dataset (clothing items) to another (handwritten digits). In this case, the target representation data is only partially labeled.
To address this challenge, the authors applied their previous findings by replacing the cost function with a generalized cost functional that can retain additional information, such as class labels. Thus, the search for optimal transport while preserving the class was reduced to the problem of finding a saddle point of the functional.
The researchers demonstrated this principle using functionals of two types: class-guided and pair-guided. The first algorithm addressed the dataset transfer problem, while the second focused on image-to-image supervised translation. The class-guided functionals were capable of constructing stochastic transport maps, where random noise is added to the input.
The authors tested the effectiveness of their approach in experiments with a variety of datasets, ranging from simple synthetic ones to biological data. A significant portion of the datasets included pairs of images from different domains. Comparisons with methods based on Euclidean functions showed that using the generalized cost functional was at least as effective, and in some cases even yielded better metrics.

The results of class-preserving mapping between FMNIST (images of clothing) to MNIST (handwritten digits) datasets. The last two rows correspond to the new method with added noise z and without it.
In conclusion, the researchers noted that although the new method performed well in tasks involving class preservation, it should be used with caution in other cases, as constructing the functional in such instances can be non-trivial.
The results of this work were presented at the ICLR 2024 conference, and a paper detailing the findings was published in its proceedings.