Marat Khamadeev
Marat Khamadeev

Russian scientists created a universal benchmark that allows one to compare methods for buildings Schrödinger Bridges
In recent years, generating images using diffusion models has become a widely used tool. These models transform noise into synthetic data samples, and from a mathematical perspective, this process resembles diffusion — the random movement of particles or molecules described by the laws of thermodynamics and statistical mechanics.
This process is based on transforming one data distribution into another — complex to simple during training and vice versa during generation. In the data space (e.g. images), this is equivalent to moving from one point to another. To optimize the models for fast performance, an optimal transport between these points is required. One way to achieve this is by using entropy-based regularization, which helps to efficiently search for a solution. This task is known as the Entropic Optimal Transport (EOT) problem.
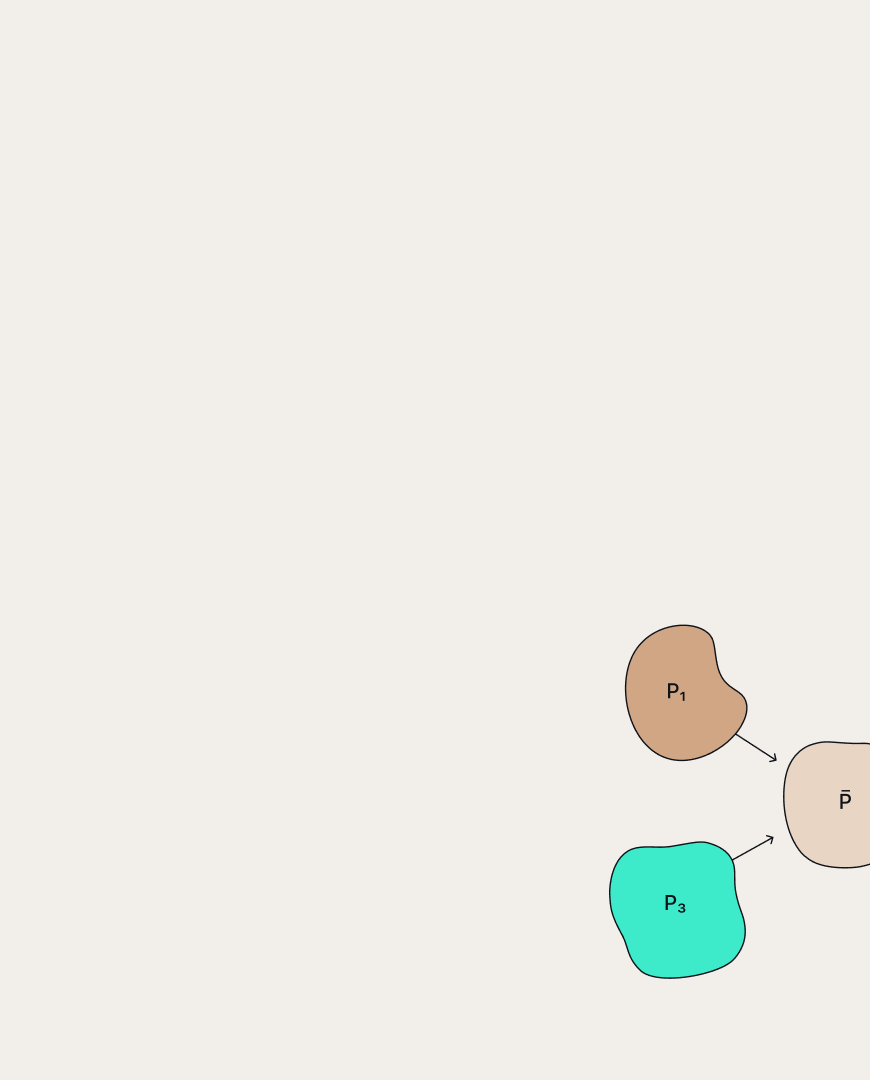
Interestingly, this problem has been around for longer than machine learning itself. In the 1930s, Erwin Schrödinger was interested in it. He is known as one of the founders of quantum mechanics, but he also worked on problems in statistical physics and Brownian motion of particles. Today, the Schrödinger Bridge (SB) is the most probable way of stochastic transition between distributions, and the problem of constructing it is equivalent to the EOT problem.
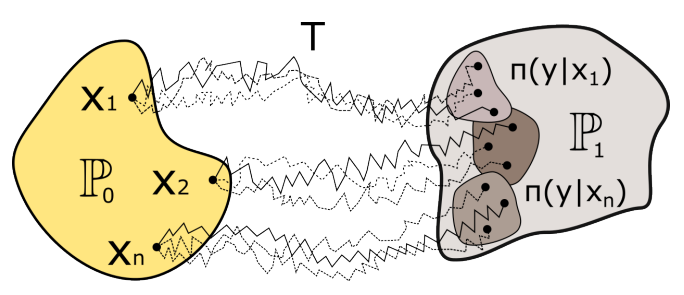
Schematic representation of the Schrödinger Bridge
Efforts of many scientific groups are directed toward finding solutions to this problem. In addition to numerical approaches, neural solvers have also proven to be useful. However, it is not always possible to determine whether the proposed algorithm properly solves EOT/SB, or whether researchers were simply lucky with their choice of parameterization, regularization, tricks, etc.
To help colleagues better evaluate their methods, a team from AIRI and Skoltech created the first-ever theoretically grounded EOT/SB benchmark. Their work is based on a new method to create continuous pairs of probability distributions with analytically known (by our construction) EOT solutions between them. The benchmark evaluates the method by comparing the solution found by it with the ground truth solution. Thanks to the genericity of the methodology, the development is suitable for a wide class of EOT/SB solvers.
The benchmark was tested on several popular neural solvers, training them on generated pairs in high-dimensional spaces, including the space of 64 × 64 celebrity faces. The effectiveness of the method was evaluated using a special metric based on the averaged and normalized Bures-Wasserstein metric.
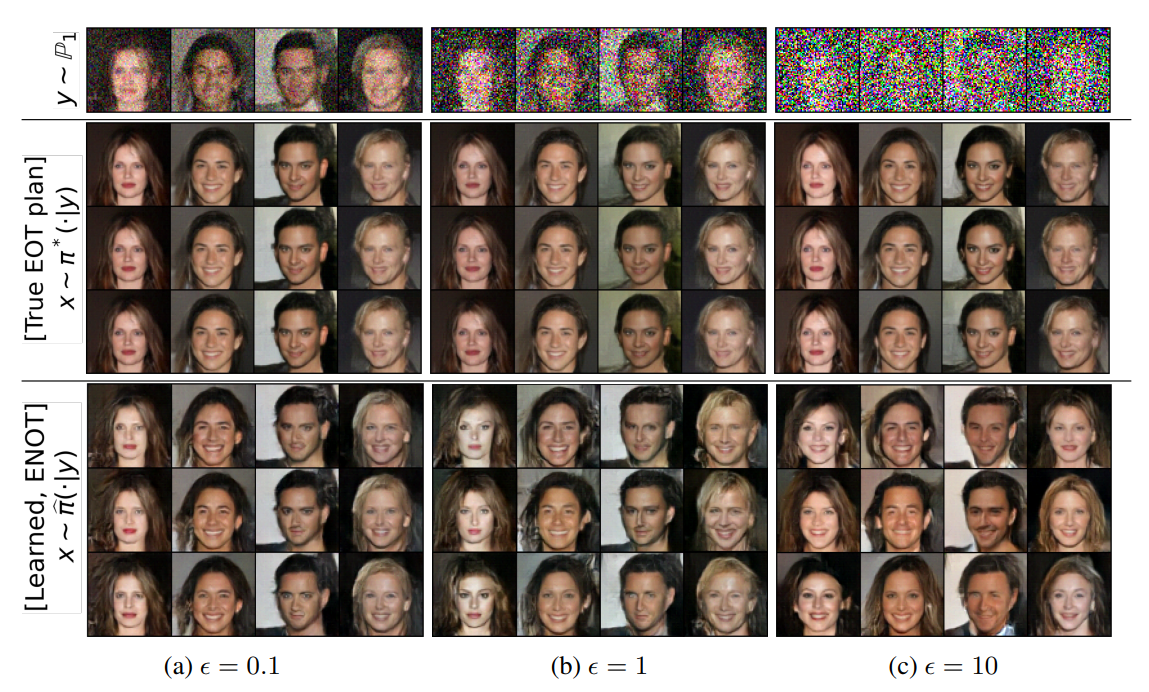
Qualitative comparison of ground truth samples with samples produced by ⌈ENOT⌋ solver. With the increase of the model’s parameter ϵ, the diversity increases but the precision of image restoration drops
We found that most solvers’ performance significantly depends on the selected hyper-parameters. At the same time, we report the results of solvers with their default configs and/or with limited tuning. We neither have deep knowledge of many solvers nor have the resources to tune them to achieve the best performance on our benchmark pairs. Therefore, the results obtained using the new benchmark are more of a kindly invitation to interested authors to improve the results for their solvers, rather than an answer to the question of which one is better.

The project code is available on GitHub, and details of the research can be found in the article published in the proceedings of the NeurIPS 2023 conference.