Marat Khamadeev
Marat Khamadeev

The star-shaped architecture will improve generation using diffusion models
If you open a bottle of perfume, its volatile compounds soon will evenly fill the room thanks to the process of diffusion. Similarly, a meaningful data structure that undergoes blurring over time gradually turns into noise. But even if an analytical distribution describes the blurring, its direct inversion — that is removing the noise — becomes computationally infeasible.
Neural networks can help in this situation. They can be trained by feeding a large dataset characterizing the process of destruction of information. Such datasets consist of pairs of data, where the first is informative, and the second is obtained from the first after several iterations of blurring. Models trained in this way are called diffusion or, more fully, denoising diffusion probabilistic models (DDPM). They are capable not only of efficiently removing noise from images or sounds but also of drawing fairly realistic pictures and illustrations.
The process of blurring data traditionally relies on Gaussian distribution, much like how gas molecules diffuse. It allows reducing the problem to Markov chains, in which the state at each stage, described by some marginal distribution, depends only on the state at the previous step. The problem is that this approach is reasonable for some types of data, such as images while injecting Gaussian noise into data distributed on manifolds, bounded volumes, or with other features can be unnatural. In some special cases, other distributions can be adapted, for example, Categorical and Gamma distributions, but there is no general solution to this problem yet.
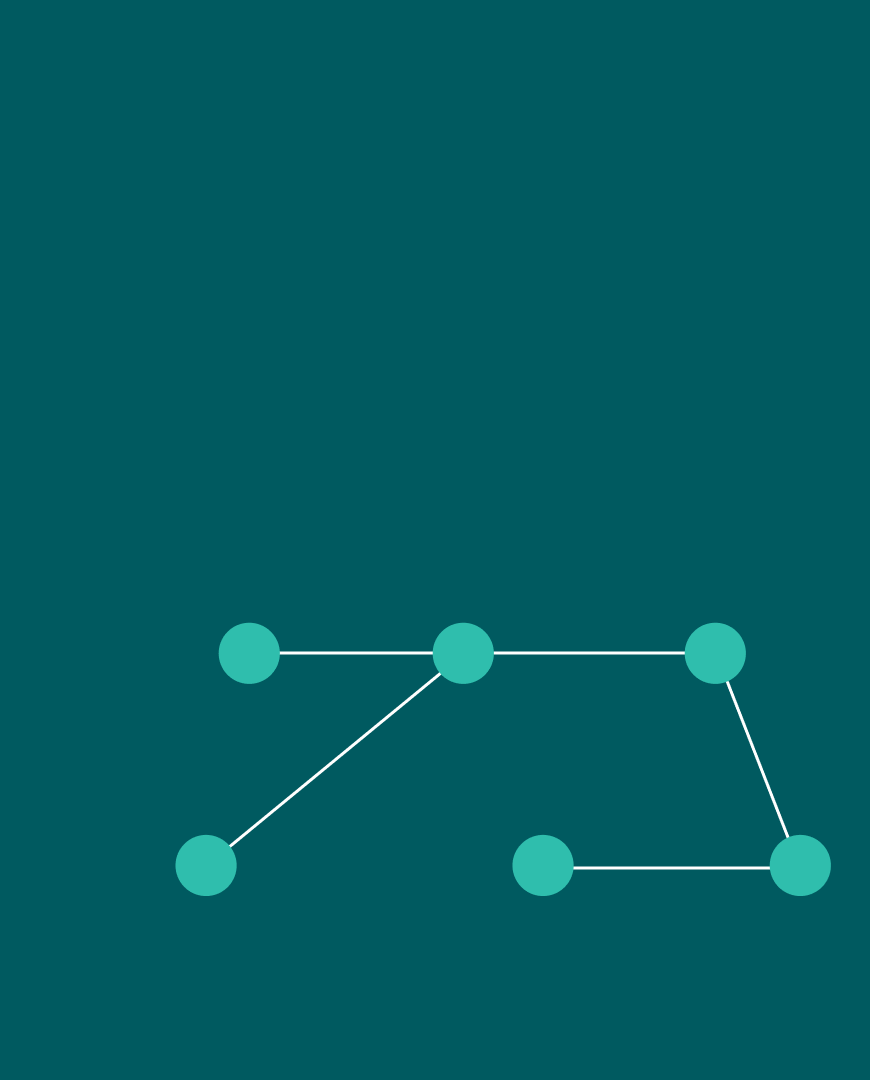
A team of scientists from Europe and Russia led by Dmitry Vetrov has directed their efforts to tackle this difficulty. Their idea is based on abandoning the Markovian architecture of the algorithm. Instead, the researchers proposed an approach in which the marginal distribution of each step remains linked to the initial distribution as the data is transformed into noise. If a Markov chain could be represented as a sequence of steps, the new approach rather resembles a star. For this reason, the authors called it Star-Shaped (SS) DDPM.
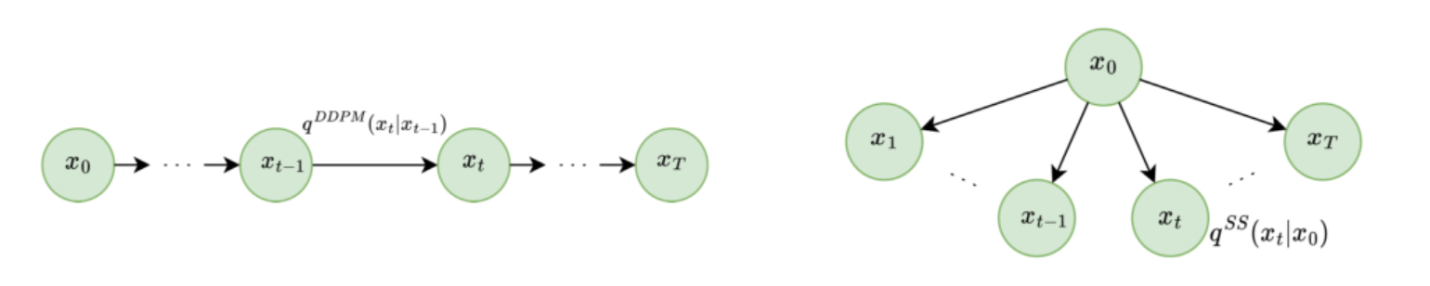
Markovian forward processes of DDPM (left) and the star-shaped forward process of SS-DDPM (right)
An important advantage SS-DDPM provides is the generalization of Gaussian DDPM to an exponential family of noise distributions. The authors confirmed this for some of them, in particular, von Mises-Fisher, Dirichlet, Wishart, and beta distributions. At the same time, the model turns out to be equivalent to DDPM in the case of Gaussian distributions.
To assess how the introduction of star-shaped architecture affects the efficiency of solving the problems, the researchers conducted a series of experiments. The evaluation included working with synthetic data generated from the probabilistic simplex and the manifold of positive-definite matrices, geodesic data (fires on the Earth's surface), categorical data (texts), as well as images. In all cases, SS-DDPM models had an advantage or were comparable to regular or improved DDPM methods.
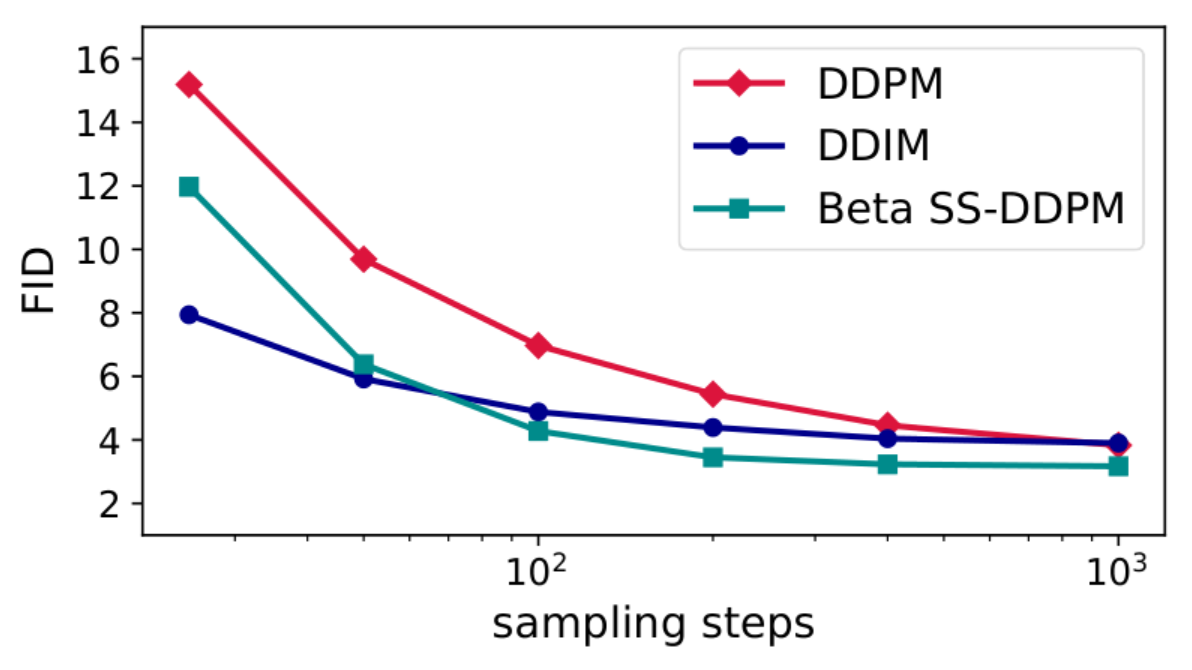
Comparison of SS-DDPM with beta distribution, regular DDPM, and its improved version DDIM using the Fréchet inception distance (FID) metric in image generation tasks
We have verified that on image data, star-shaped diffusion with Beta distributed noise attains comparable performance to Gaussian DDPM. This fact indicates that the use of a Gaussian distribution may not be the most optimal, which means that diffusion models can still be improved. For our part, we hope in the future to find an opportunity to generalize SS-DDPM to a wider class of distributions than the exponential family
The model’s code is open source and available on GitHub. Details of the study can be found in the article published in the proceedings of the NeurIPS 2023 conference.