How machine learning helps robots navigate obstacles

Pathfinding problem naturally arise in various applications like robotics, video games and others. In the most common case, we are interested in the shortest path that bypasses obstacles. In AI this problem is often reduced to finding a path on a graph representing the agent's workspace. The most common type of graph used in practice is a 8-connected grid, which is regular tessellation of the workspace into the blocked and free (square) cells. For finding a path on a grid A* algorithm is the golden standard.

A* is a heuristic search algorithm. It iteratively explores the search space. The performance of A* heavily depends on the heuristic function given as an input to the algorithm. This function estimates distance to the goal node and is used to focus the search to the goal.

For grid graphs, several popular heuristics have been proposed, such as Octile Distance, that not only guarantees finding a solution but also ensures that it will be optimal. But the major drawback of using Octile Distance or other similar heuristics is that they don't take obstacles into account. That means, in the obstacle-rich environments A* might suffer fr om poor performance due to extensive exploration of the search space. Ideally we want to have a perfect heuristic that for every node knows the exact cost of the shortest path circumnavigating all of the obstacles to the goal.

In order to obtain the accurate approximation of the perfect instant dependent heuristic function that takes obstacles into account the research team fr om Federal Research Center for Computer Science and Control of RAS and AIRI (Daniil Kirilenko, Anton Andreychuk, Aleksandr Panov, and Konstantin Yakovlev) utilized the state-of-the-art machine learning techniques. Using modern neural networks (namely, transformers), the researchers proposed to predict two types of heuristic functions.

The first type of heuristic is the correction factor (CF) which is defined as the ratio of the value of the available instanced independent heuristic to the value of the perfect heuristic. Unlike learning the absolute values of the cost-to-go heuristic function, which was known before, learning the correction factor utilizes the knowledge of the instance-independent heuristic.

The second type of heuristic is a path probability map (PPM). It is designed to demonstrate how likely the node is lying on the shortest path from the start to the goal. This heuristic can be employed in the Focal Search framework as the secondary one, allowing us to preserve the guarantees on the bounded sub-optimality of the solution.

The architecture of the model that researchers use to predict proposed heuristics has three main blocks: a convolutional encoder, a spatial transformer, and a convolutional decoder. The convolutional encoder utilizes the well-known ResNet blocks and is aimed at extracting the local features of the pathfidning instance such as corners of the obstacles, narrow passages etc. The transformer leverages the mechanism of self-attention to establish the global relations between these features (how important is one feature with reference to the other). Finally, the transformed feature maps are processed by the convolutional decoder, which provides the final output.

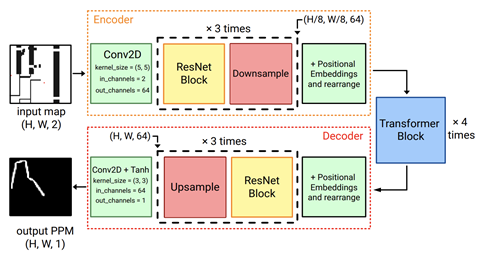
The network is quite small and includes only 1 million parameters. The team trained each model using direct supervision with mean squared error as a training signal.

The authors conducted a thorough empirical evaluation on a comprehensive dataset of planning tasks. Experiments showed that the suggested techniques reduce the computational effort of the A* up to a factor of 4x while producing the solutions, whose costs exceed those of the optimal solutions by less than 0.3% on average. It also outperform the competitors, which include the conventional techniques from the heuristic search, i.e. weighted A* (WA*), as well as the state-of-the-art learnable planners. Latter includes the planner from Takahashi et al. (A*+HL) that tries to predict perfect cost-to-go heuristic and the planner from of Yonetani et al. (Neural A*) that exploits differentiable version of the A* to predict cost of the certain moves.

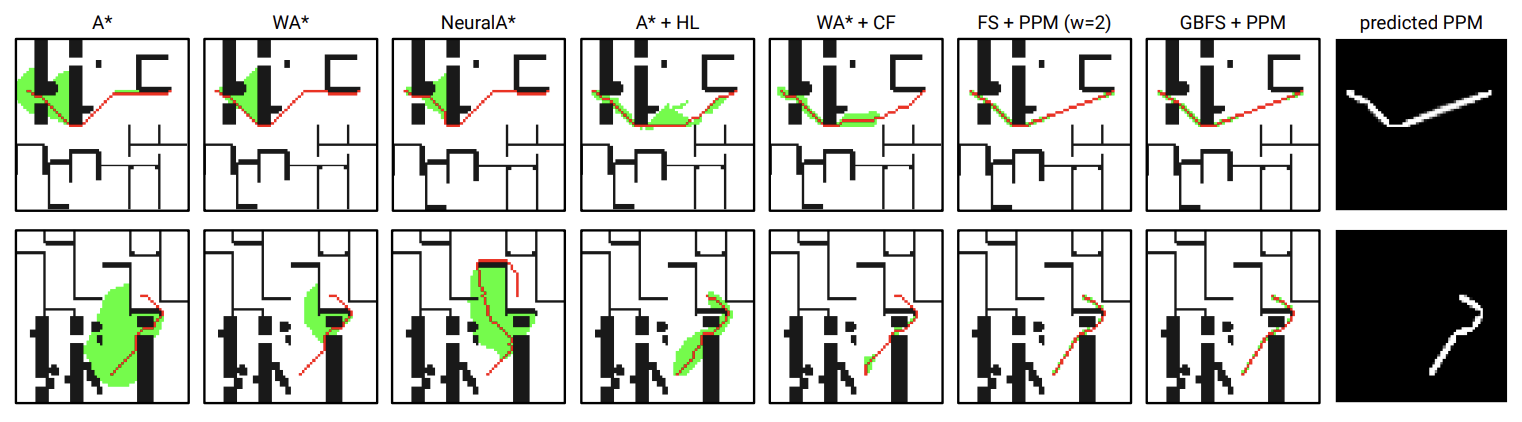
Several examples of the pathfinding results. The expanded nodes are shown in green, and the path in red. The last column shows the predicted PPMs.

The avenues for future research of the team include planning in 3D, planning with kinodynamic constraints (including sample-based planning) and much more.