Marat Khamadeev
Marat Khamadeev

Tensor trains helped to make gradient-free optimization more efficient
Optimization is a fundamental task in many machine learning algorithms, which typically involves finding the minimum or maximum of a function with multiple variables. One of the earliest approaches to solving this problem was gradient descent, which involves moving from a point on a multi-dimensional surface formed by a function towards its decreasing direction indicated by the gradient taken with the opposite sign.
Despite being proposed in the 19th century, gradient descent remains an extremely popular method in machine learning and data analysis due to its simplicity. However, the method becomes computationally complex when optimizing models with a large number of parameters, which can lead to getting stuck in local minima. In some cases, it may be impossible to calculate the gradient.
For this reason, researchers are actively developing gradient-free optimization methods based on other mathematical principles. One of the research directions involves discretization of functions from a continuous argument and finding the minimum or maximum element in an implicitly given multi-dimensional array (tensor). Methods for decomposing high-dimensional tensors into a tensor train (TT), which represents them as a product of several low-dimensional tensors, play an important role in bypassing the curse of dimensionality. Approaches such as TTOpt and Optima-TT, as well as their modifications, have already demonstrated their effectiveness in gradient-free optimization tasks, so this area of research is constantly evolving.
Earlier, we reported how a team of researchers from AIRI and Skoltech led by Ivan Oseledets made tensor train decomposition faster and more accurate. This time, the researchers used this decomposition to solve a gradient-free optimization problem for a multi-dimensional black-box function. The peculiarity of this problem is that researchers have no information about the structure of such a black box, including whether this function is differentiable, and the high dimensionality makes it difficult to use traditional methods. Such situations are increasingly encountered in areas dealing with Big Data.
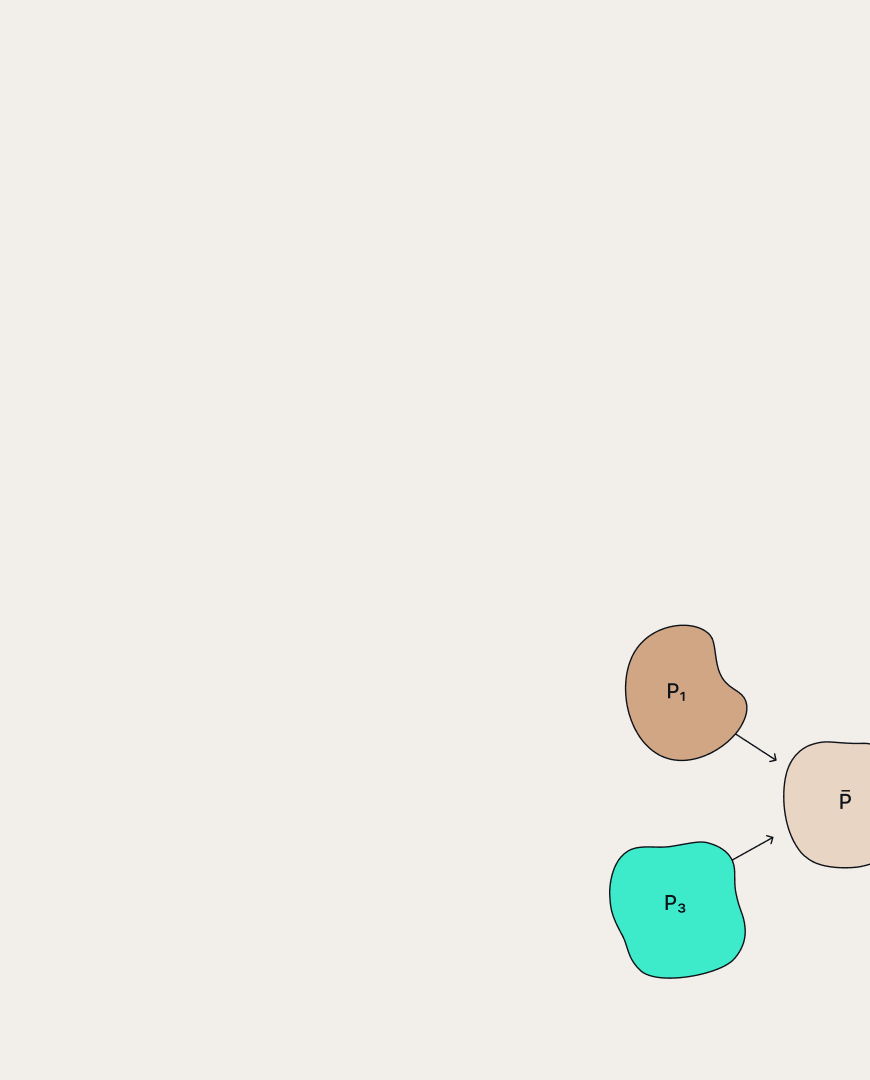
The new method is based on sampling several vectors from a probability tensor represented in the TT format. These vectors are fed into the black box, which calculates their function value, after which a special algorithm selects a subset of candidates from the output values according to a certain criterion. These candidates are used to update the original tensor by minimizing the loss function, which is composed of the sum of logarithms of probabilities at selected points. For this reason, the method is called Probabilistic Optimization with Tensor Sampling (PROTES).
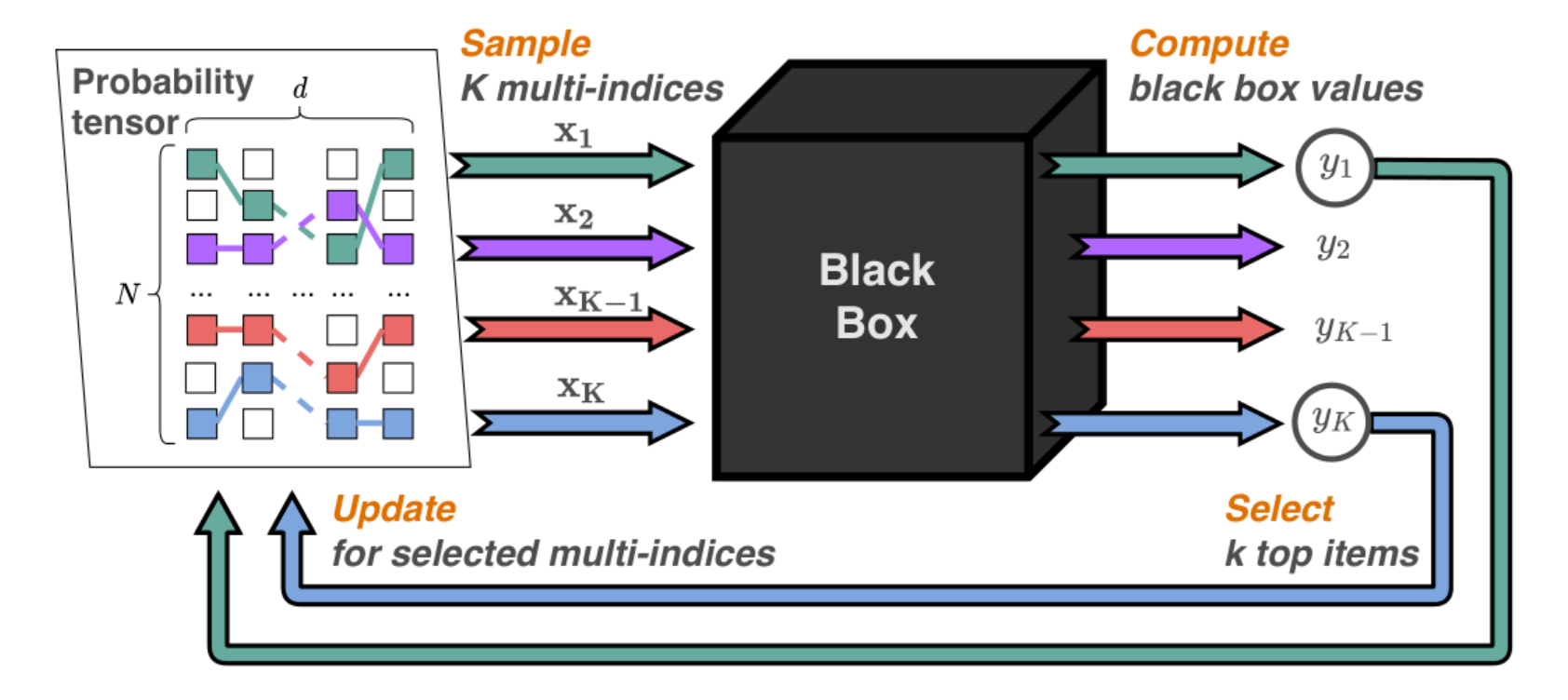
Schematic representation of the proposed optimization method PROTES
The authors tested the new approach on 20 model problems, including quadratic unconstrained binary optimization and optimal control problems. The results were compared with seven popular optimization methods, both classical and modern, and also ones based on tensor decomposition. The experiments showed that PROTES demonstrates an advantage in most tasks.
At this stage, our method is more heuristic. We have focused more on its practical application to fairly diverse and interesting problems than on strict theoretical justification. We still have to make estimates of convergence, ranks, number of operations, and much more in the future.

The source code of the proposed method and numerical examples are available in a public repository, and details of the research can be found in an article published in the proceedings of the NeurIPS 2023 conference.